10. Derivatives and Tangent Lines
c. Derivative as a Function
1. Definition
So far we have computed the derivative of a function, \(f(x)\), at \(x=a\) where \(a\) is an actual number, obtaining a number, \(f'(a)\). However, what happens if we let \(a\) be a variable? Then we obtain \(f'(a)\) as a function of \(a\). If we replace the \(a\) by an \(x\), then we obtain the following definition of the derivative of \(f(x)\) as a function:
The derivative of the function \(f(x)\) is the function \(f'(x)\) given by the limit: \[ f'(x)=\lim_{h\rightarrow 0} \dfrac{f(x+h)-f(x)}{h} \] The figure shows the tangent line as a function of position. The slopes are the derivative function.
We can also write the derivative, \(f'(x)\), using the limit of a difference quotient, but then we also need to replace the limit variable since it was previously \(x\):
The derivative of the function \(f(x)\) can also be written as the limit: \[ f'(x)=\lim_{z\rightarrow x} \dfrac{f(z)-f(x)}{z-x} \]
The derivative of a function \(y=f(x)\) can be written in either prime notation or differential notation: \[ f'(x)=\dfrac{df}{dx}=\dfrac{dy}{dx} \] The differential notation reminds us of the difference quotient definition: \[ \dfrac{df}{dx}=\lim_{\Delta x\to0}\dfrac{\Delta f}{\Delta x} \]
If \(f(x)=x^2\), find its derivative \(\dfrac{df}{dx}\). Use it to find \(\dfrac{df}{dx}(3)\).
We write out and compute the limit definition, using expand and cancel: \[\begin{aligned} \dfrac{df}{dx}&=\lim_{h\rightarrow 0} \dfrac{f(x+h)-f(x)}{h} =\lim_{h\rightarrow 0} \dfrac{(x+h)^2-(x)^2}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{x^2+2xh+h^2-x^2}{h} =\lim_{h\rightarrow 0} \dfrac{2xh+h^2}{h} \\ &=\lim_{h\rightarrow 0} (2x+h) =2x \end{aligned}\]
This time we use the alternate formula, using factor and cancel: \[\begin{aligned} \dfrac{df}{dx}&=\lim_{z\rightarrow x} \dfrac{f(z)-f(x)}{z-x} =\lim_{z\rightarrow x} \dfrac{z^2-x^2}{z-x} \\ &=\lim_{z\rightarrow x} \dfrac{(z-x)(z+x)}{z-x} =\lim_{z\rightarrow x} (z+x) =2x \end{aligned}\]
Using \(\dfrac{df}{dx}=2x\), we find \(\dfrac{df}{dx}(3)=6\). This is the same answer we found in a previous example.
If \(f(x)=\dfrac{3}{x}\), find its derivative \(f'(x)\). Use it to find \(f'(6)\).
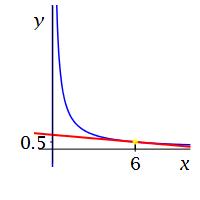
\(\begin{aligned} f'(x)&=-\,\dfrac{3}{x^2} \\ f'(6)&=-\,\dfrac{1}{12} \end{aligned}\)
We write out and compute the limit definition: \[\begin{aligned} f'(x)&=\lim_{h\rightarrow 0} \dfrac{f(x+h)-f(x)}{h} =\lim_{h\rightarrow 0} \dfrac{\dfrac{3}{x+h}-\dfrac{3}{x}}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{1}{h}\dfrac{3x-3(x+h)}{x(x+h)} =\lim_{h\rightarrow 0} \dfrac{-3h}{xh(x+h)} \\ &=\lim_{h\rightarrow 0} \dfrac{-3}{x(x+h)} =-\,\dfrac{3}{x^2} \end{aligned}\]
This time we use the alternate formula: \[\begin{aligned} f'(x)&=\lim_{z\rightarrow x} \dfrac{f(z)-f(x)}{z-x} =\lim_{z\rightarrow x} \dfrac{\dfrac{3}{z}-\dfrac{3}{x}}{z-x} \\ &=\lim_{z\rightarrow x} \dfrac{1}{z-x}\dfrac{3x-3z}{zx} =\lim_{z\rightarrow x} \dfrac{-3}{zx} =-\,\dfrac{3}{x^2} \end{aligned}\]
Using \(f'(x)=-\,\dfrac{3}{x^2}\), we find \(f'(6)=-\,\dfrac{3}{36}=-\,\dfrac{1}{12}\). This is the same answer we found in a previous exercise.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum